Cómo arreglar una mesa que cojea, según las matemáticas
A todos nos ha pasado alguna vez: te sientas frente a una mesa, en un bar, una terraza, un restaurante... y una de las patas cojea. ¿Qué hacer? La solución universal es de sobra conocida: doblar un papel o un trozo de cartón para fijar la pata renqueante. Mal. Según las matemáticas, hay una solución mejor.
El problema lo explica (con gran felicidad y genial acento alemán) el profesor Matthias Kreck, de la Universidad de Bonn, y es un estupendo ejemplo de cómo un buen matemático afronta un problema cotidiano.
La hipótesis de partida es que las 4 patas de la mesa son iguales y la mesa es un cuadrado perfecto. El problema está en el suelo, que no es plano. Para resolverlo, en lugar de colocar un papel bajo la pata que cojea, lo mejor es rotar la mesa en círculo menos de 90º, menos de un cuarto de giro completo. En algún punto, rotando a un lado u otro, generalmente solo unos centímetros, encontraremos el lugar exacto donde hay completa estabilidad. Y no, no es casualidad: hay una explicación matemática que demuestra que eso siempre ocurre así.
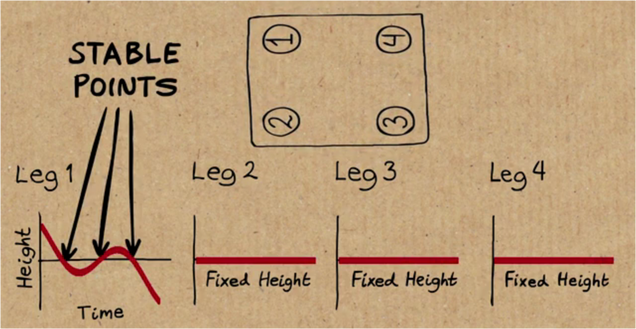
Matthias Kreck lo explica en el vídeo debajo a golpe de fórmulas, con papel y lápiz, y hay hasta un informe detallado publicado al respecto hace años. La explicación matemática consiste en medir la distancia de la pata que cojea al suelo cada vez que rotamos ligeramente la mesa. Modelando esos valores en función del tiempo y la altura, obtendremos que se cumple el llamado teorema del valor intermedio, que establece que si tenemos una función continua entre dos puntos, uno positivo (distancia positiva entre la pata y el suelo, es decir, cojea) y otro negativo (distancia negativa entre la pata y el suelo - la pata roza de forma excesiva), habrá necesariamente un punto en el que esa distancia sea cero, es decir, la mesa será perfectamente estable.
Puedes ver la explicación completa debajo y, aunque está en inglés, se entiende muy bien paso a paso, dibujos y fórmulas incluidas. La próxima vez que te encuentres ante una mesa que cojea y se cumplan los puntos de partida mencionados, prueba. Si no funciona, algo falla. Pero no serán las matemáticas.
El problema lo explica (con gran felicidad y genial acento alemán) el profesor Matthias Kreck, de la Universidad de Bonn, y es un estupendo ejemplo de cómo un buen matemático afronta un problema cotidiano.
La hipótesis de partida es que las 4 patas de la mesa son iguales y la mesa es un cuadrado perfecto. El problema está en el suelo, que no es plano. Para resolverlo, en lugar de colocar un papel bajo la pata que cojea, lo mejor es rotar la mesa en círculo menos de 90º, menos de un cuarto de giro completo. En algún punto, rotando a un lado u otro, generalmente solo unos centímetros, encontraremos el lugar exacto donde hay completa estabilidad. Y no, no es casualidad: hay una explicación matemática que demuestra que eso siempre ocurre así.
Matthias Kreck lo explica en el vídeo debajo a golpe de fórmulas, con papel y lápiz, y hay hasta un informe detallado publicado al respecto hace años. La explicación matemática consiste en medir la distancia de la pata que cojea al suelo cada vez que rotamos ligeramente la mesa. Modelando esos valores en función del tiempo y la altura, obtendremos que se cumple el llamado teorema del valor intermedio, que establece que si tenemos una función continua entre dos puntos, uno positivo (distancia positiva entre la pata y el suelo, es decir, cojea) y otro negativo (distancia negativa entre la pata y el suelo - la pata roza de forma excesiva), habrá necesariamente un punto en el que esa distancia sea cero, es decir, la mesa será perfectamente estable.

Puedes ver la explicación completa debajo y, aunque está en inglés, se entiende muy bien paso a paso, dibujos y fórmulas incluidas. La próxima vez que te encuentres ante una mesa que cojea y se cumplan los puntos de partida mencionados, prueba. Si no funciona, algo falla. Pero no serán las matemáticas.
[vía Numberphile]
***

Comentarios
Publicar un comentario